Mathematics Quiz Discrete
1 / 1 pts
Suppose you have an endorelation on a set. If you turned that endorelation into a graph, you would always find that the degree of each vertex must be less than the cardinality of the set.
Correct!
True
False
0 / 1 pts
If you represented a symmetric relation as a graph, what feature(s) would that graph be guaranteed to have? Check all that apply.
The graph would be weighted.
The graph would be directed.
You Answered
The graph would be unweighted.
Correct!
The graph would be undirected.
The graph would be connected.
The graph would be disconnected.
The graph would have at least one cycle.
The graph would not have any cycles.
Original Score: 1 / 1 pts
If two vertices in a graph are connected, that means they have an edge between them.
True
Correct!
False
1 / 1 pts
All graphs have at least one edge.
True
Correct!
False
1 / 1 pts
If you have a free tree, adding any additional edge to it makes it no longer a free tree.
Correct!
True
False
1 / 1 pts
If you have a free tree, removing any edge from it makes it no longer a free tree.
Correct!
True
False
0 / 1 pts
The set of all rooted trees is a subset of the set of all binary search trees.
You Answered
True
False
1 / 1 pts
All graphs are connected graphs.
True
Correct!
False
1 / 1 pts
Suppose you had a free tree, and turned it into a rooted tree. It would have the same height no matter which node you chose to make the root.
True
Correct!
False
1 / 1 pts
The leaves of a (rooted) tree will always be at the same depth.
True
Correct!
False
1 / 1 pts
Every node in a (rooted) tree will always have exactly one parent, except the root, which never has a parent.
Correct!
True
False
1 / 1 pts
On Twitter, a user can “follow” another user without being followed in return. (For instance, I follow R pioneer and statistician Hadley Wickham, but he is way too famous to follow me.) Also, when you “follow” someone, you just plain follow them — you don’t “super follow” them, or “barely follow” them.
Is the Twitter graph (where users are vertices, and edges represent “followings” between users) a directed or undirected graph? And is it weighted or unweighted?
directed and weighted
Correct!
directed and unweighted
undirected and weighted
undirected and unweighted
Original Score: 1 / 1 pts Regraded Score: 1 / 1 pts
This question has been regraded.
A website called Ubermapquest has a giant GIS graph of all vehicular intersections in all seven continents of the world. (Not really, but pretend.) This graph has information about how many kilometers are between each vehicular intersection, and whether the route between them is traversable in both directions or only one. (For instance, in downtown Fredericksburg, you can drive directly on a one-way street from Caroline & William to Caroline & Amelia, but not the other way.)
Is the Ubermapquest graph (where vertices are intersections, and edges are driveable paths between them) directed or undirected? Is it weighted or unweighted? Is it connected or disconnected?
directed, weighted, and connected
Correct!
directed, weighted, and disconnected
directed, unweighted, and connected
directed, unweighted, and disconnected
undirected, weighted, and connected
undirected, weighted, and disconnected
undirected, unweighted, and connected
undirected, unweighted, and disconnected
0 / 3 pts
What is the total distance of all the edges in the minimal spanning tree of the graph below?
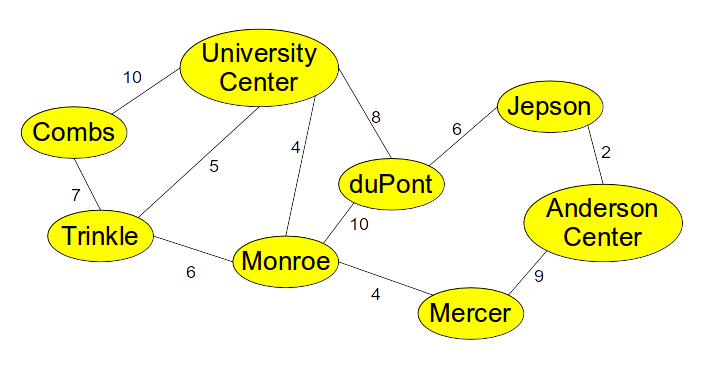
You Answered
Correct Answers
36.0 (with margin: 0.0)
1.5 / 1.5 pts
What order would the nodes in the following binary tree be visited if it were traversed in pre-order? (Type the letters as capitals, with no spaces or other punctuation, like this: SWAGDEYHUP. That’s not the actual correct answer, of course.)
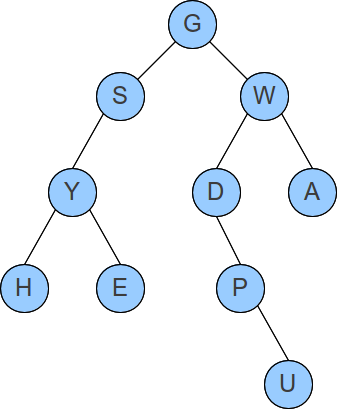
Correct!
Correct Answers
GSYHEWDPUA
0 / 1.5 pts
What order would the nodes in the above binary tree be visited if it were traversed in-order? (Type your answer in the same way.)
You Answered
Correct Answers
HYESGDPUWA
1 / 1 pts
What order would the nodes in the above binary tree be visited if it were traversed in post-order? (Type your answer in the same way.)
Correct!
Correct Answers
HEYSUPDAWG