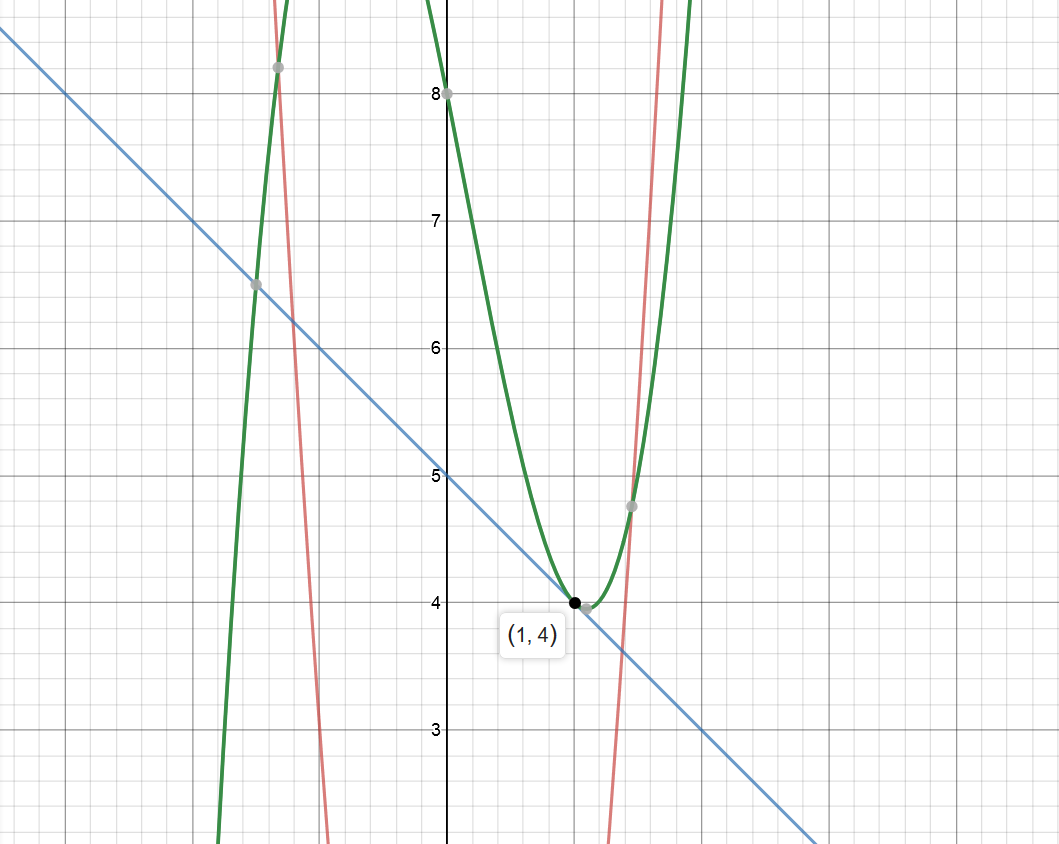
Find a function whose second derivative is y” = 12x – 2 at each point (x,y) on its graph and y = -x+5
Find a function whose second derivative is y” = 12x – 2 at each point (x,y) on its graph and y = -x+5 is tangent to the graph at the point corresponding to x = 1.
This problem has multiple pieces, but follows the basic initial value problem model–although nothing designates this as a physics problem, I will use
![]() and
and ![]() as initial values for ease of labeling.
as initial values for ease of labeling.
So to start attacking this problem, we are taking y” as an entering argument to solve for y. The first thing we need to do is find y’ by integration
![]()
Basic integration procedures from early calculus lead us to the indefinite solution
![]()
in solving for c we can rewrite this equation as
![]()
At this point we pause and focus on the tangent line y=-x+5. To be tangent to the curve y for which we are solving, they must match in instantaneous rate of change. To have the same slope at the same point, the derivative at the given point x=1 must match. for the tangent line, the derivative is y=-1 at every point, since it is a straight line. If we set the two equations equal to each other,
![]()
we can substitute 1 for x and solve for the initial value in y’ (v0)
![]()
or simplified
![]()
continuing
![]()
and subtract 4 from both sides.
![]()
So
![]()
Integrating again
![]()
or
![]()
The second stipulation for the the line y=-x+5 to be a tangent line is that it touches the curve on the y function at the given point x=1
plugging 1 into the tangent line
![]()
If we set 4 equal to the function y
![]()
![]()
![]()
add to both sides and you get
![]()
so
![]()
graph!